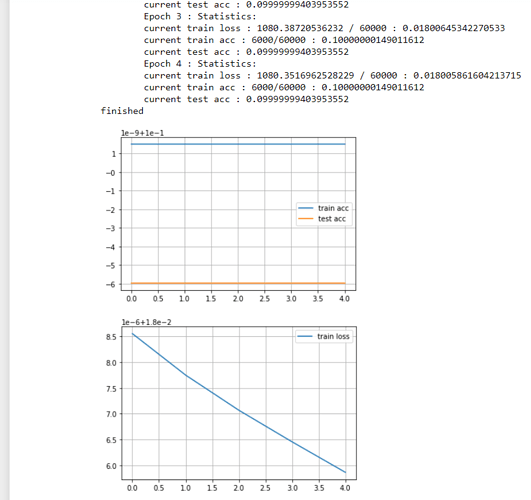
Am I correct in thinking that there is some implicit rounding down of dimensions going on when the integer division by the stride would leave a remainder?
The base formula for the width of the output representation of a convolution layer is given by (width_of_input - filter_size + 2*padding) / stride + 1
Taking the first NiN block as an example, the input is a 224x224 large image. This layer has a 11x11 kernel with stride of 4, and padding explicitly set to 0 (the 1x1 conv layers shouldn’t change the dimension so I ignore them here). The above formula gives (224 - 11)/4 + 1 as the output dimension, which would give 54.25 - I see the output shape from the dimensions test in the textbook chapter is 54.
The same thing happens for many other layers in the network - an imperfect division by a stride. When this happens, does PyTorch implicitly crop some columns from the left/right/top/bottom at random to make it round down?
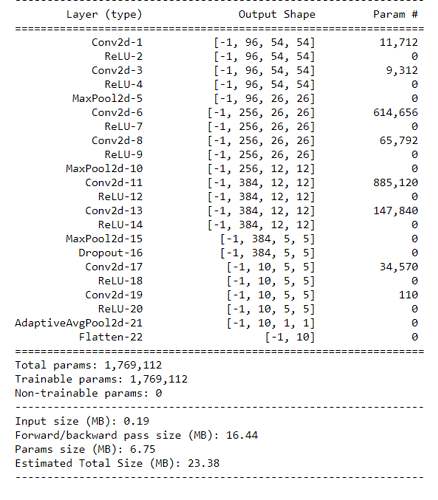
Unrelatedly, here are my calculations for the resource usage of the NiN in the textbook chapter:
INPUT: 224 x 224 x 1 ACTIVS: 224 * 224 PARAMS: 0
CONV(1,96,11,4,0) ACTIVS: 96 * 54 * 54 PARAMS: (11*11*1)*96
CONV(96,96,1,1,0) ACTIVS: 96 * 54 * 54 PARAMS: (1*1*96)*96
CONV(96,96,1,1,0) ACTIVS: 96 * 54 * 54 PARAMS: (1*1*96)*96
MaxPool(3,2) ACTIVS: 96 * 26 * 26 PARAMS: 0
NiNBlock(96,256,5,1,2) ACTIVS: 3*(256 * 26 * 26) PARAMS: 256 * (256+256+(5*5*96))
MaxPool(3,2) ACTIVS: 256 * 12 * 12 PARAMS: 0
NiNBlock(256,384,3,1,1) ACTIVS: 3*(384 * 12 * 12) PARAMS: 384 * (384+384+(3*3*256))
MaxPool(3,2) ACTIVS: 384 * 5 * 5 PARAMS: 0
Dropout ACTIVS: 384 * 5 * 5 PARAMS: 0
NiNBlock(384,10,3,1,1) ACTIVS: 3*(10 * 5 * 5) PARAMS: 10 * (10+10+(3*3*384))
AdaptiveMaxPool ACTIVS: 10 PARAMS: 0
Flatten ACTIVS: 10 PARAMS: 0
When training: we need 2 * the ACTIVS sum (values + gradients), and 3 * the PARAMS sum (values, gradients, and a cache for momentum/Adam)
When testing: we just need the sum of activs + params. If we’re being clever we can erase previous ACTIVS as we go, so we only need the sum of the largest two consecutive ACTIVS. We also don’t need the Dropout ACTIVS.
Hey @Nish, great question. I am not exactly sure which edge does PyTorch choose to round down. However, if you use some level of padding, it won’t lose any information since you just remove that edge’s padding away.
Any idea on q2 why are there two 1x1 layers ?
Has anybody used pytorch_lightning ?
For exercise 3 part 1, considering only a single call of nin_block, would it be correct to say that for k=kernel_size, c=out_channels, that there are c(2+k**2) floating point values, being the parameters of the single block? This comes from there being k**2 weights for each kernel with c kernels in a filter resulting in ck**2, and from there being two fully connected layers, each with c singular kernels.
Also, what does “amount of computation” mean?
Exercises
-
Tune the hyperparameters to improve the classification accuracy.
- its not tuning based on stuff, I feel like lr=0.1 is not working for me. How to find effiecient lr, should be explored in the chapter.
training nin
training normal network with the same methods works
sample_net = nn.Sequential(nn.Conv2d(1, 32, kernel_size=3,padding=1),
nn.ReLU(),
nn.Conv2d(32, 64, kernel_size=3, padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2),
nn.Dropout(p=0.25),
nn.Flatten(),
nn.Linear(64 * 14 * 14, 128),nn.ReLU(), nn.Dropout(p=0.5),
nn.Linear(128, 10)
)
```
gives me an accuracy of 83.
So I am thinking its a learning rate issue. But how do I find an optimium lr.
-
Why are there two 1 Ă— 1 convolutional layers in the NiN block? Remove one of them, and then observe and analyze the experimental phenomena.
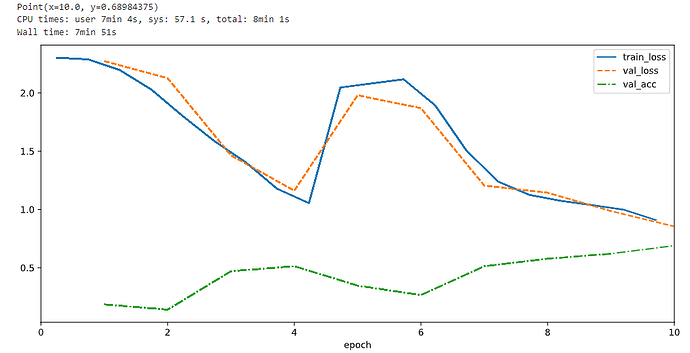
- Not able to train 1x1 I dunno
-
Calculate the resource usage for NiN.
- How do you calculate this. I have been seeing this question for past few exercises.
-
What is the number of parameters?
-
What is the amount of computation?
-
What is the amount of memory needed during training?
-
What is the amount of memory needed during prediction?
-
What are possible problems with reducing the 384 Ă— 5 Ă— 5 representation to a 10 Ă— 5 Ă— 5 representation in one step.
- the size would lead to certain problems likelosing intermediate conv layer info.
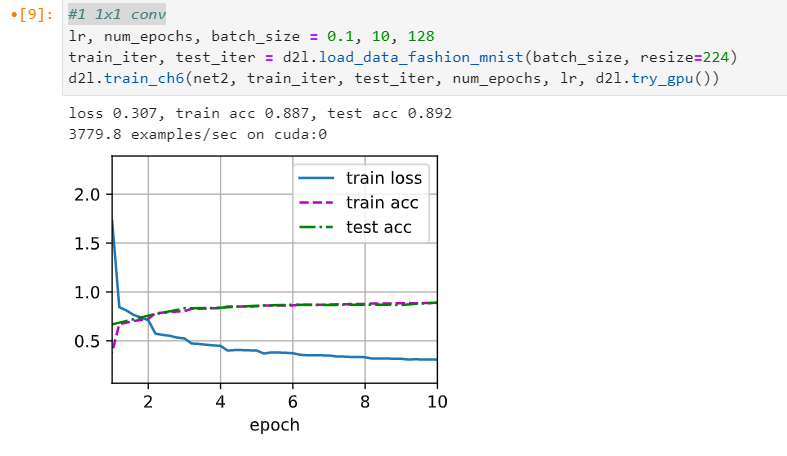
As for Exe-2, intuitively with only one 11 conv layer, we get reduced representative capability, such as c = a^b. However I experimented with only one conv11 layer in each NiN block.
However I got even better result: loss 0.364, train acc 0.868, test acc 0.858. Is it as expected?
Anyone know why does the author use 1x1 conv layer instead of any difference conv layer ? what the actually purpose of it?
@thainq NiN replaces fully-connected output layers with 1x1 convolutions to reduce the number of parameters and hence prevent overfitting. The inspiration was probably the same as when fully-connected image-representation layers were first replaced by convolutions in models like LeNet (or Neocognitron 
?). As a result, we have an equivalent or even better model with fewer parameters.
Q: Why are there two 1x1 convolutional layers per NiN block? Increase their number to three. Reduce their number to one. What changes?
Here is my take on this question:
The 3x3 convolution acts as the first layer of the “micro” network, so with two 1x1 convolutions we get a three layer fully-connected micro network. As far as I remember reading somewhere, fc nets with more than three hidden layers get really hard to train and do not provide much improvement, hence the need for other architectures. So probably using two 1x1 convolutions is somewhat the optimal limit.
Reducing to number of 1x1 convolutions to one should in theory reduce the expressiveness of the micro network, but we still have a two layer net which might be quite enough.
I think that using the pattern 1x1 + 3x3 + 1x1 for a “bottleneck residual block” (see Fig.5 from the ResNet paper) is quite common these days. The first 1x1 convolution reduces the number of channels for the expensive 3x3 and the second 1x1 has a dual purpose:
- it up-scales the channels
- we get a micro two layer fc net
For example see the PixelRNN paper (https://arxiv.org/pdf/1601.06759.pdf), Figure 5.
Would love to hear other opinions!