Sep '20
input is 3 dimensions, why does norm_shape use the last two dimensions of the input in the example ,but the last one in the final trainning. normalized_shape is input.size()[1:], but in the trainning, normalized_shape is input.size()[-1]. what’s the difference? why change?
Oct '20
▶ HeartSea15
Oct '20
▶ StevenJokess
I used pytorch. May I ask you a question about two different methods? Mxnet’s method is right and wrong in pytorch. The following changes should be made.
1 reply
Oct '20
▶ HeartSea15
Oct '20
▶ goldpiggy
Can LN be done in a single dim? such as tensor with shape [2,3,4], could the LN be done in norm_shape=shape[1] (3)?
1 reply
Oct '20
▶ foreverlms
Hi @foreverlms, great question. Yes Layernorm can be done at a single dim, which will be the last dimension. See more details at pytorch documentation: “If a single integer is used, it is treated as a singleton list, and this module will normalize over the last dimension which is expected to be of that specific size.”
Feb '21
Book content is very helpful for those who want to learn Deep learning from scratch however
request you to please add more graphical presentation / images. It will helpful to understand concept easily.
Apr '21
▶ min_xu
Hi @min_xu, I am not fully understand your question… but in general you can imagine that the attention layer has seen a lot example start with “BOS”. As a result, it will predict “BOS” as the first token.
Apr '21
thank you , i find the code process what i thinking. mask the data after the timesteps when the model is trainning
thank you !
1 reply
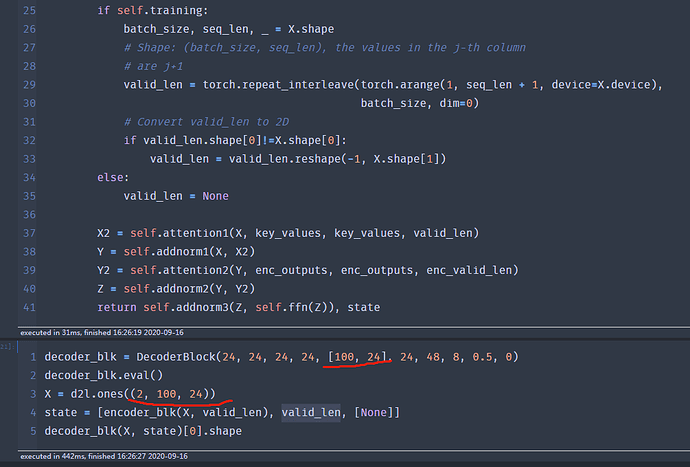
Jul '21
In decoder block there is
self.attention = d2l.MultiHeadAttention(key_size, query_size,
value_size, num_hiddens,
num_heads, dropout, use_bias)
...
self.ffn = PositionWiseFFN(ffn_num_input, ffn_num_hiddens,
num_hiddens)
According to the paper Attention Is All You Need, the ffn has width [d_model, ?, d_model] where d_model is the embedding size of a token. But in the above code num_hiddens is used as both the embedding size and the embedding size in attention block (the dimensionality of an input after the linear map in multi-head attention). It is not the best way to implement it if I’m correct.
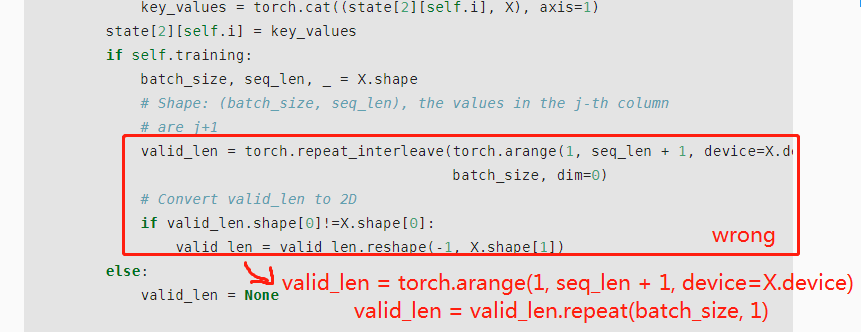
Jul '21
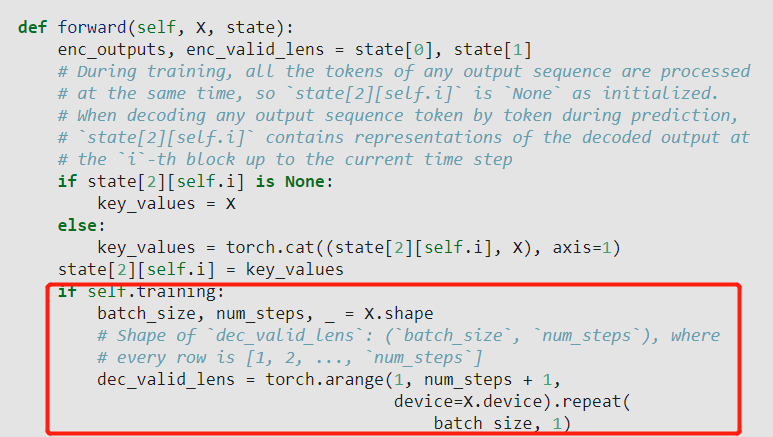
class DecoderBlock
...
def forward(...)
...
if self.training:
...
dec_valid_lens = torch.arange(1, num_steps + 1, device=X.device).repeat(batch_size, 1)
else:
dec_valid_lens = None
I’m not sure this is true. In both cases (train and inference) decoder self-attention needs two masks: padding and causal (other possible names: look-ahead or auto-regression). For convenience, they are usually combined into one tensor during calculations.
Nov '21
▶ HeartSea15
Hi @HeartSea15, are you using PyCharm? Awesome color scheme, may I know how to get it? Thanks.
Jan '22
When predicting, target tokens are feed into the Decoder one by one. At this point the num_steps is considered to be 1, that is, each time you enter a tensor of the shape torch.Size([1, 1, num_hiddens]), this will result in the position encoding of each token being the same, i.e., the position encoding fails at prediction
1 reply
Jan '22
the reason of multiplying each element by sqrt(num_hiddens) is the use of the Xavier_unifom_ to initialize parameters of the Embedding, each element is very small compared to 1/-1. (see the following figure) ,but no Xavier_unifom_ is used here…
Reference:http://nlp.seas.harvard.edu/2018/04/03/attention.html
2 replies
Feb '22
▶ guan-zi
看懂了,此处X先进行嵌入然后进行缩放,传入位置编码对象中,进行Add&Norm操作
Jan '23
▶ guan-zi
According to the paper (sec 3.4) the weights of the embedding layer are multiplied by \sqrt(d_{model}).
Mar '23
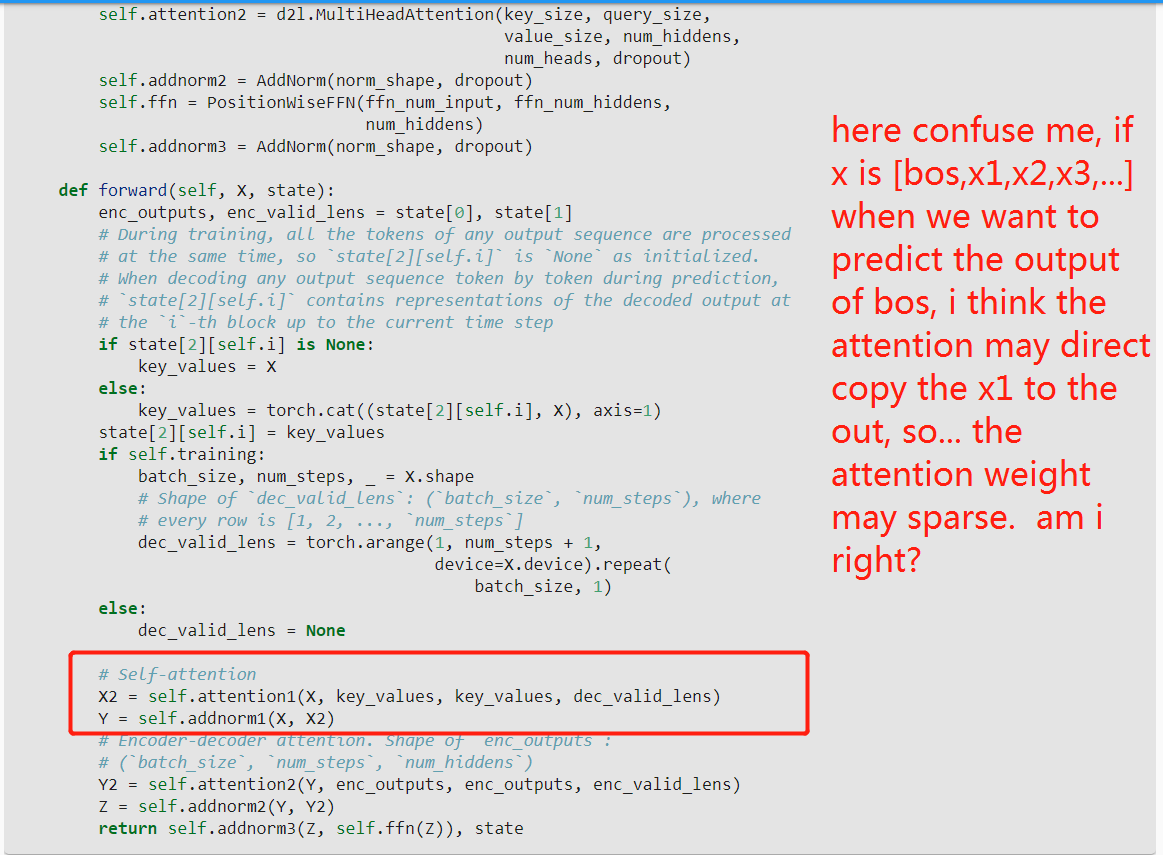
As we described earlier in this section, in the masked multi-head decoder self-attention (the first sublayer), queries, keys, and values all come from the outputs of the previous decoder layer…
I thought queries were from the previous decoder layer, while keys and values were from the last encoder layer. Is the above statement true?
1 reply
Apr '23
▶ LilNeo
Same doubt. Have you figured it out how to solve this problem? Or any more information could be provided for me to grasp a better understanding?
Thx
Sep '23
My solutions to the exs: 11.7
Sep '23
Since we use the fixed positional encoding whose values are always between -1 and 1, we multiply values of the learnable input embeddings by the square root of the embedding dimension to rescale before summing up the input embedding and the positional encoding.
It makes sense intuitively that we should make a balance between the magnitudes of the input embedding and the positional encoding before adding them. But why should we scale the input embedding by exactly the square root of its dimension?
Nov '23
▶ ubayram
The second sublayer uses the encoder output as keys and values, while the first sublayer uses q, k, and v from the previous decoder layer.
Nov '23
Hi,
I do not understand the state[2][i] very much in the TransformerDecoder. I think it just concatenates all of the past queries and the current query of the first attention sublayer at the i-th decoder block. Why is it needed? Why not just use the current query? Thank you very much!
3 replies
Nov '23
▶ LilNeo
the reason of multiplying each element by sqrt(num_hiddens) is the use of the Xavier_unifom_ to initialize parameters of the Embedding, each element is very small compared to 1/-1.
I did not find a statement indicating that the reason is the use of the Xavier_uniform from the post you linked. It does not explain the reason. I think your screenshot just shows that the model uses Xavier_unifom_ to initialize the model’s weights.
Below is a screenshot of this part in the link you provided.
Dec '23
▶ Bo_Yang
I also not understand state[2][i] in DecoderBlock. Why concat X and state[2][I] to become key_values and and feed concat result to MHAttention(X, key_values, key_values)?
Feb '24
▶ min_xu
the logistic in both training step and prediction step are coherent, ie. input ‘token i’ against kv pairs “[bos,token 2,…, token i-1, token i” to predict ‘token i+1’
Feb '24
▶ Bo_Yang
I think it means that the self-attention tries hard to reuse the predicted historical tokens/features ( or say ‘last context’ but not entire context ) to give an insight
Mar '24
I might have missed something here, but shouldn’t there be a softmax layer for the output of the decoder? In the end, the decoder should return a probability vector for vocab. If I understand it correctly, the current decoder only returns a linear combination of weights, which are not guaranteed to be probabilities. Thanks.
Mar '24
▶ LilNeo
So shouldn’t we do this in practice in our tutorial?
Aug '24
▶ Bo_Yang

I adjusted the naming and handling of state [2] in this forwards() function, but without any changes of its original processing logic. I think after this adjustment, it may be easier to understand.
class TransformerDecoderBlock(nn.Module):
def forward(self, X, state):
enc_outputs, enc_valid_lens, dec_key_values = state[0], state[1], state[2]
if dec_key_values[self.i] is None: # training mode, or first token in prediction mode
dec_key_values[self.i] = X
else: # other tokens in prediction mode
dec_key_values[self.i] = torch.cat((dec_key_values[self.i], X), dim=1)
# state[2][self.i] = key_values
...
# Self-attention
X2 = self.attention1(X, dec_key_values[self.i], dec_key_values[self.i], dec_valid_lens)
...
return self.addnorm3(Z, self.ffn(Z)), (enc_outputs, enc_valid_lens, dec_key_values)
In fact, state[2] or dec_key_values, is a list(length=num_blks) of tensor, and the shape of the tensor is (batch_size, num_steps, num_hiddens).
Each TransformerDecoderBlock maintains one of these tensors, to record the target tokens it has seen before during prediction(or the all target tokens in training). And then, the tensor will be used to the first self-attention as key_values in its own DecoderBlock.
Dec '24

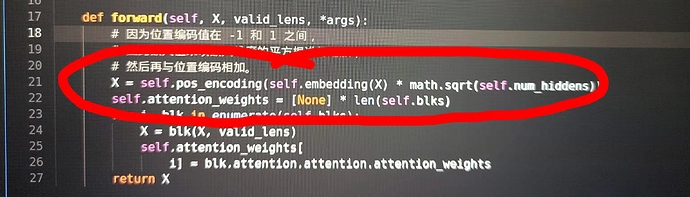
When predicting, target tokens are feed into the Decoder one by one. So the position info of target tokens are missing in Decoder, and the position encoding will fail also.
Obviously, it’s a bug.
The solution could be as follows:
SUMMARY: pass the position info into Decoder with token, and make PositionalEncoding to use it
Only requires three simple steps:
- d2l.EncoderDecoder.predict_step(), pass the position info to Decoder.
from:
for _ in range(num_steps):
Y, dec_state = self.decoder(outputs[-1], dec_state)
change to:
for idx in range(num_steps):
Y, dec_state = self.decoder(outputs[-1], dec_state, offset=idx)
- TransformerDecoder.forward(), pass offset to PositionalEncoding.
from:
def forward(self, X, state):
X = self.pos_encoding(self.embedding(X) * math.sqrt(self.num_hiddens))
change to:
def forward(self, X, state, offset=0):
X = self.pos_encoding(self.embedding(X) * math.sqrt(self.num_hiddens), offset)
- PositionalEncoding.forward(), calculate with offset.
from:
def forward(self, X):
X = X + self.P[:, :X.shape[1], :].to(X.device)
change to:
def forward(self, X, offset=0):
X = X + self.P[:, offset:offset+X.shape[1], :].to(X.device)
This solution should be the most intuitive and simple solution with minimal modifications to the original framework.